The Diffie-Hellman key exchange algorithm is a method to securely establish a shared secret between two parties (Alice and Bob). Elliptic-curve Diffie–Hellman (ECDH) allows the two parties, each having an elliptic-curve public–private key pair, to establish the shared secret. This shared secret may be directly used as a key, or to derive another key. The key, or the derived key, can then be used to encrypt subsequent communications using a symmetric-key cipher. It is a variant of the Diffie–Hellman protocol using elliptic-curve cryptography.
Diffie-Hellman
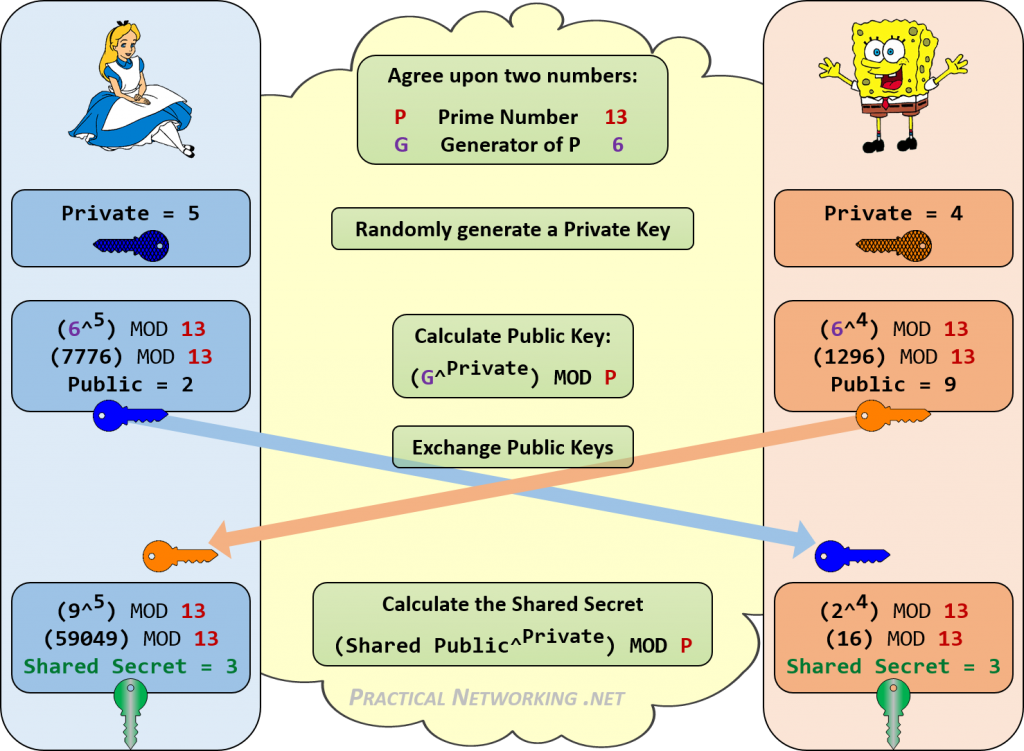
The Diffie-Hellman key exchange is a way for people to secretly share information. When two people want to use cryptography, they often only have an insecure channel to exchange information. Martin Hellman, Whitfield Diffie and Ralph Merkle developed a protocol that allows this information exchange over an insecure channel. The resulting protocol has become known as Diffie-Hellman key exchange. Sometimes it is called Diffie-Hellman key agreement, Diffie-Hellman key establishment, Diffie-Hellman key negotiation or Exponential key exchange. Using this protocol, both parties agree on a secret key. They use this key to encrypt their communication using a symmetric-key cipher.
The scheme was first published by Whitfield Diffie and Martin Hellman in 1976. Diffie-Hellman key agreement itself is an anonymous (non-authenticated) key-agreement protocol, it provides the basis for a variety of authenticated protocols, and is used to provide perfect forward secrecy in Transport Layer Security’s short-lived modes.
Elliptic-curve cryptography
We can find elliptic curves cryptosystems in TLS, PGP and SSH, which are just three of the main technologies on which the modern web and IT world are based. Not to mention Bitcoin and other cryptocurrencies.
Elliptic-curve cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. ECC requires smaller keys compared to non-EC cryptography (based on plain Galois fields) to provide equivalent security. In mathematics, an elliptic curve is a plane algebraic curve defined by an equation of the form: y² = x³ + ax + b.
The primary advantage of using Elliptic Curve based cryptography is reduced key size and hence speed. Elliptic curve based algorithms use significantly smaller key sizes than their non elliptic curve equivalents. The difference in equivalent key sizes increases dramatically as the key sizes increase. The approximate equivalence in security strength for symmetric algorithms compared to standard asymmetric algorithms and elliptic curve algorithms is shown in the table below.
| Symmetric Key Length | Standard asymmetric Key Length | Elliptic Curve Key Length |
|---|---|---|
| 80 | 1024 | 160 |
| 112 | 2048 | 224 |
| 128 | 3072 | 256 |
| 192 | 7680 | 384 |
| 256 | 15360 | 512 |
As can be seen, to get equivalent strength to a 256 bit symmetric key, a standard asymmetric algorithm would have to use an enormous key of 15360 bits. Keys of this size are typically not practical due to the amount of processing power that would be required, and therefore the speed of the operations. However, with elliptic curve algorithms, the equivalent key length is 512 bits, which is entirely practical.
If you want to know more about the curves you can go here: SafeCurves: choosing safe curves for elliptic-curve cryptography.
ECDiffieHellmanCng Class
Provides a Cryptography Next Generation (CNG) implementation of the Elliptic Curve Diffie-Hellman (ECDH) algorithm. This class is used to perform cryptographic operations. A basic example could be as follows:
ECDiffieHellmanCng alice = new ECDiffieHellmanCng();
alice.KeyDerivationFunction = ECDiffieHellmanKeyDerivationFunction.Hash;
alice.HashAlgorithm = CngAlgorithm.Sha256;
ECDiffieHellmanCng bob = new ECDiffieHellmanCng();
bob.KeyDerivationFunction = ECDiffieHellmanKeyDerivationFunction.Hash;
bob.HashAlgorithm = CngAlgorithm.Sha256;
byte[] bobKey = bob.DeriveKeyMaterial(alice.PublicKey);
byte[] aliceKey = alice.DeriveKeyMaterial(bob.PublicKey);
After running this code, aliceKey and bobKey are both 32 bytes long and match each other. Now, Alice could use this as a symmetric key:
AesCryptoServiceProvider aes = new AesCryptoServiceProvider();
aes.Key = aliceKey;
Easy! right? right! the problem here is that ECDiffieHellmanCng is not available (yet) on mono either on linux or macos, look here https://github.com/mono/mono/issues/9037 and here: https://github.com/mono/mono/issues/9463.
So… What can we do?
The Legion of the Bouncy Castle to the rescue!

Originally, in the late 1990s, the Legion of the Bouncy Castle was simply a number of individuals united both in their interests of Cryptography and Open Source. The first official release of the Bouncy Castle APIs appeared in May 2000 and was about 27,000 lines long. The project grew steadily with a C# version of the Java APIs being added in 2006. By 2012 with the Java code base well past 300,000 lines and the C# one over 140,000 it started becoming obvious that a bit more organisation was required to maintain both progress and the quality of the APIs.
On 18 October 2013, a not-for-profit association, the Legion of the Bouncy Castle Inc. was established in the state of Victoria, Australia, by the core developers and others to take ownership of the project and support the ongoing development of the APIs. The association was recognised as an Australian charity with a purpose of advancement in education and a purpose that is beneficial to the community by the Australian Charities and Not-For-Profits Commission on 7 November 2013. The association was authorised to fundraise to support its purposes on 29 November 2013 by Consumer Affairs Victoria.
Let’s write some code
While I was trying to reduce the minimum .NET required version for SILENTTRINITY I realized that it could be possible to run the stager by replacing the ECDiffieHellmanCng implementation for a portable one. I most admit this was really hard, but I finally did it after a lot of reading and thanks to the BouncyCastle c# libraries.
I’m using the portable package: Portable.BouncyCastle
PM> Install-Package Portable.BouncyCastle -Version 1.8.5
This is the basic method:
public static byte[] KeyExchange(Uri url)
{
X9ECParameters x9EC = NistNamedCurves.GetByName("P-521");
ECDomainParameters ecDomain = new ECDomainParameters(x9EC.Curve, x9EC.G, x9EC.N, x9EC.H, x9EC.GetSeed());
AsymmetricCipherKeyPair aliceKeyPair = GenerateKeyPair( ecDomain);
ECPublicKeyParameters alicePublicKey = (ECPublicKeyParameters)aliceKeyPair.Public;
ECPublicKeyParameters bobPublicKey = GetBobPublicKey(url, x9EC, alicePublicKey);
byte[] AESKey = GenerateAESKey(bobPublicKey, aliceKeyPair.Private);
return AESKey;
}
The first step is to get the curve and the parameters:
X9ECParameters x9EC = NistNamedCurves.GetByName("P-521");
ECDomainParameters ecDomain = new ECDomainParameters(x9EC.Curve, x9EC.G, x9EC.N, x9EC.H, x9EC.GetSeed());
P-521 reffers to secp521r1, it’s the default curve for the ECDiffieHellmanCng class. With those values we can create the domain parameters.
To generate the key pair we’re using this method:
private static AsymmetricCipherKeyPair GenerateKeyPair(ECDomainParameters ecDomain)
{
ECKeyPairGenerator g = (ECKeyPairGenerator)GeneratorUtilities.GetKeyPairGenerator("ECDH");
g.Init(new ECKeyGenerationParameters(ecDomain, new SecureRandom()));
AsymmetricCipherKeyPair aliceKeyPair = g.GenerateKeyPair();
return aliceKeyPair;
}
We’ll need the aliceKeyPair to share the public key to Bob and then be able to derive the Bob’s public key:
ECPublicKeyParameters alicePublicKey = (ECPublicKeyParameters)aliceKeyPair.Public;
Now, we’re going deep into the funny part… The whole idea of this is to find a secure shared key, so Bob needs to send me his public keys. Bob can acheive this by several ways. I would prefer to wait a binary stream from Bob, but it seems this is not a common practice. The common practice is to send a xml file with X and Y coordinates and receive the same.
private static ECPublicKeyParameters GetBobPublicKey(Uri url,
X9ECParameters x9EC,
ECPublicKeyParameters alicePublicKey)
{
KeyCoords bobCoords = GetBobCoords(url, alicePublicKey);
var point = x9EC.Curve.CreatePoint(bobCoords.X, bobCoords.Y);
return new ECPublicKeyParameters("ECDH", point, SecObjectIdentifiers.SecP521r1);
}
private static KeyCoords GetBobCoords(Uri url, ECPublicKeyParameters publicKey)
{
string xml = GetXmlString(publicKey);
string responseXml = Encoding.UTF8.GetString(Http.Post(url, Encoding.UTF8.GetBytes(xml)));
XmlDocument doc = new XmlDocument();
doc.LoadXml(responseXml);
XmlElement root = doc.DocumentElement;
XmlNodeList elemList = doc.DocumentElement.GetElementsByTagName("PublicKey");
return new KeyCoords {
X = new BigInteger(elemList[0].FirstChild.Attributes["Value"].Value),
Y = new BigInteger(elemList[0].LastChild.Attributes["Value"].Value)
};
}
private static string GetXmlString(ECPublicKeyParameters publicKeyParameters)
{
string publicKeyXmlTemplate = @"<ECDHKeyValue xmlns=""http://www.w3.org/2001/04/xmldsig-more#"">
<DomainParameters>
<NamedCurve URN=""urn:oid:1.3.132.0.35"" />
</DomainParameters>
<PublicKey>
<X Value=""X_VALUE"" xsi:type=""PrimeFieldElemType"" xmlns:xsi=""http://www.w3.org/2001/XMLSchema-instance"" />
<Y Value=""Y_VALUE"" xsi:type=""PrimeFieldElemType"" xmlns:xsi=""http://www.w3.org/2001/XMLSchema-instance"" />
</PublicKey>
</ECDHKeyValue>";
string xml = publicKeyXmlTemplate;
xml = xml.Replace("X_VALUE", publicKeyParameters.Q.AffineXCoord.ToBigInteger().ToString());
xml = xml.Replace("Y_VALUE", publicKeyParameters.Q.AffineYCoord.ToBigInteger().ToString());
return xml;
}
internal class KeyCoords
{
public BigInteger X { get; set; }
public BigInteger Y { get; set; }
}
Note: Http.Post is a self-implementation to send POST requests.
First, in GetBobCoords we’re building a xml to send our coordinates (GetXmlString)… so Bob responds with his public key’s coordinates and we’re returning the coordinates; from these coordinates, we’re creating a Point:
var point = x9EC.Curve.CreatePoint(bobCoords.X, bobCoords.Y);
return new ECPublicKeyParameters("ECDH", point, SecObjectIdentifiers.SecP521r1);
CreatePoint will throws an exception if the point isn’t inside the curve which it is good, because we’re going to know if we’re doing something wrong. Now, we have both public keys and Alice’s private key. We need to generate a shared key to encrypt/decrypt the communication; for this, we’re going to derive the Bobs key using a SHA256 function based on Alice’s private key.
private static byte[] GenerateAESKey(ECPublicKeyParameters bobPublicKey,
AsymmetricKeyParameter alicePrivateKey)
{
IBasicAgreement aKeyAgree = AgreementUtilities.GetBasicAgreement("ECDH");
aKeyAgree.Init(alicePrivateKey);
BigInteger sharedSecret = aKeyAgree.CalculateAgreement(bobPublicKey);
byte[] sharedSecretBytes = sharedSecret.ToByteArray();
IDigest digest = new Sha256Digest();
byte[] symmetricKey = new byte[digest.GetDigestSize()];
digest.BlockUpdate(sharedSecretBytes, 0, sharedSecretBytes.Length);
digest.DoFinal(symmetricKey, 0);
return symmetricKey;
}
In cryptography, a key-agreement protocol is a protocol whereby two or more parties can agree on a key in such a way that both influence the outcome. If properly done, this precludes undesired third parties from forcing a key choice on the agreeing parties. Protocols that are useful in practice also do not reveal to any eavesdropping party what key has been agreed upon. Many key exchange systems have one party generate the key, and simply send that key to the other party – the other party has no influence on the key. Using a key-agreement protocol avoids some of the key distribution problems associated with such systems. Protocols where both parties influence the final derived key are the only way to implement perfect forward secrecy.
We’re using ECDH and initializing the agreement using Alice’s private key. After getting the shared key’s bytes we’re getting a symmetric key:
IDigest digest = new Sha256Digest();
byte[] symmetricKey = new byte[digest.GetDigestSize()];
digest.BlockUpdate(sharedSecretBytes, 0, sharedSecretBytes.Length);
digest.DoFinal(symmetricKey, 0);
Cool… now we can encrypt the communications! Let’s try it:
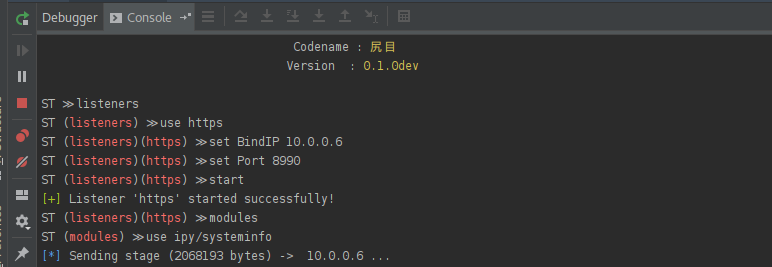
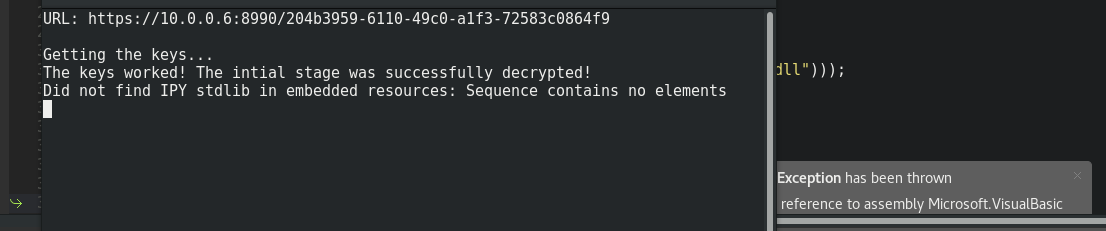
It worked!
Final thoughts
Well, this is awesome! This implementation should run on Linux, MacOS and Xamarin (Android and iOS). Also we can obfuscate the code using ConfuserEx from Linux. Using HTTPS between Alice and Bob should be the standard. I’m going to keep learning more about this topic. I’m glad to hear a better way to do this.